Пользователи столкнулись с "неразрешимой" математической загадкой
Пользователь портала Reddit поделился математической головоломкой, у которой, по его мнению, нет решения. Об этом пишет издание Mirror.

Мужчина обратился к пользователям портала Reddit с просьбой помочь ему решить странную задачу. Оказалось, что все находят решения разными способами и ответы у всех получатся разные. Пользователь также отметил, что картинку он нашел на тропинке во время прогулки, а в углу была надпись «Чемпион мира: ___».
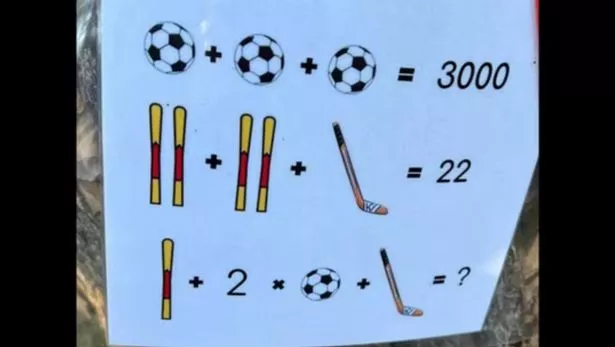
На картинке изображены уравнения, в которых вместо переменных используются картинки - лыжи, мячи и клюшки.
Мужчина предположил, что лыжи во втором уравнении должны делиться на два, то есть 2, 4, 6, 8 или 10. Это означало, по его мнению, что окончательное уравнение должно быть 2019, 2016, 2013, 2010 или 2007.
«Если я предположу, что они ищут чемпиона мира по футболу, то 2010 — единственный год из всех вариантов, когда проводился Кубок ФИФА, поэтому ответом будет Испания. Это основное предположение, что они ищут футбольного чемпиона. Я что-то упускаю или в головоломке не хватает детали?»
Некоторые люди предлагали в комментариях свои варианты решения:
«Например, если вы возьмете: a + b + c = 10, a - b + c = 12, a + c =? Если мы попытаемся решить первые два уравнения, вы обнаружите, что столкнулись с той же проблемой. Но если мы выполним уравнение 1 + уравнение 2, мы получим 2a + 2c = 22, что дает a+c = 11. Таким образом, даже не имея возможности найти точные значения a и c, мы можем найти +с».
«Что здесь происходит? В примере, который я привел, три уравнения линейно зависимы, что означает, что вы можете составить любое из уравнений, объединив два других уравнения. Но на фото в посте у нас 3a = 3000, 4b+c = 22, 2a+b+c = ? Вы обнаружите, что не можете объединить уравнения, чтобы добраться до третьего. Почему?»
«Представьте коэффициенты каждого уравнения в виде векторов: (3,0,0), (0,4,1), (2,1,1). Теперь, если мы объединим первые два: x(3,0,0) + y(0,4,1) = (3x, 4y, y) = (2,1,1) тогда x = 2/3 Но тогда мы имеем 4y = 1 И y=1. Это невозможно. Поэтому они линейно независимы Это означает, что третье уравнение, по сути, несет в себе информацию, которой нет в результате объединения двух других уравнений. Теперь мы, вероятно, сможем решить это или получить небольшой, но счетный набор решений, если предположим, что переменные являются строго целыми числами».
Кто-то еще прокомментировал: «Это не неразрешимое уравнение, на самом деле оно имеет решения, проблема в том, что существует бесконечное количество решений. Если мы рассмотрим третье уравнение, мы поставим знак вопроса вместо x, тогда a=1000, b=(22-c) /4, c=4(x-4011/2)/5. Опять же, x может быть чем угодно. Последнее уравнение ничего не исправляет, потому что добавляет еще одну переменную».
Спор подытожил человек, написавший: «С точки зрения математики — да. С точки зрения здравого смысла, 2007 год — единственный ответ, который имеет смысл».
Фото-головоломка смутила пользователей соцсетей: найдете ли вы бриллиант